The 'beauticians' and 'changelings' of physics

What do physicists mean when they talk about beauty?

On this Thanksgiving weekend, I present a post about physics and beauty to bring a little enchantment into our lives at a time of encroaching American Darkness. Now, as Trump stacks his administration with anti-science advocates and pseudo-science peddlers, we need to highlight the power, and the delights, of science.

*

Physicists talk a lot about beauty. For Nobel Prize winner Frank Wilczek,

nature is nothing less than a work of art which calls on us to assess if it is a successful work or art?” – a task he takes as tantamount to asking: “Is the world beautiful?”

In a current essay for Templeton Ideas, I consider Wilczek’s claim that nature is a work of art and ask ‘What do physicists mean when they talk about beauty?’ In this Substack I want to explore the topic from a slightly different angle.

Wilczek is among a long line of physicists who’ve regarded beauty as an ideal that the the laws of nature, and thus nature itself, ought to emulate. Fellow beauticians, as I call them, include Herman Weyl (founder of modern gauge theories of particles and forces), Paul Dirac (whose equations predicted antimatter), James Clerk Maxwell (father of electromagnetic field theory), and Johannes Kepler (who discovered the laws of planetary motion, thus laying the groundwork for Newton’s law of gravity.)

But what exactly is it that physicists consider “beautiful”?

After all, aesthetic conceptions are far from universal. In my homeland Australia, artifacts made by Aboriginal peoples weren’t seen as having any aesthetic appeal until quite recently. Now, Aboriginal art is sought after on the international art-market precisely because it defies Western visual conventions. Visiting the immense (plundered) collection of Congolese artifacts in the Humboldt Museum in Berlin is to be transported into a domain of almost-alien power which renders the niceties of European stylings pale by comparison. None of this work fits into the framework that beautician physicists value.

When these physicists talk about beauty they have in mind very specific qualities – chief among them is symmetry.

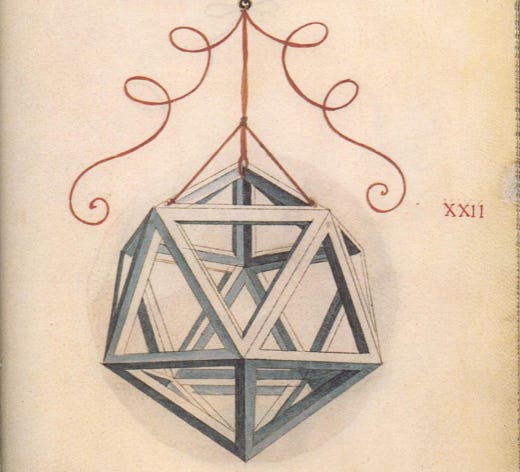
We encounter symmetry in the bilateralism of vertebrates, the six-fold patterns of snowflakes, the structures of crystals, and the bifold elegance of a butterfly’s wings. The Leonardo drawing at the start of this piece is of a three-dimensional form called an icosahedron, one of a family of 3D shapes with symmetries related to the sphere. Like many Renaissance artists, Leonardo was fascinated by such geometric structures and the regularity they embodied. It’s this kind of internal “rigor” – this crystalline order – that physics beauticians are looking for.

Most of us think about symmetry in terms of physical shapes and reflections, but mathematicians have generalized the notion to encompass many more exotic relationships, which they encode in abstract equations and theories. The ‘Platonic solids’ Leonardo so loved are described by a branch of math known as group theory, which turns out to apply to vast other areas of the world both in nature and technology. Subatomic particles are described by certain kinds of symmetry ‘groups’ and this area of math is essential to digital cryptography.

Mathematical equations encoding symmetries can offer insights into physical phenomena that would not have been easy to discover by purely observational or experimental means.

Take perhaps the most famous example: antimatter. In 1928 Dirac wrote down a relativistic equation for the electron. He found that it had two solutions: one positive, the other negative, as often happens in math, where, say 5 and -5 are legitimate solutions to an equation.

What to do about the negative electron solution? At first Dirac ignored it, but Oppenheimer suggested it might portend the existence of an actual particle, a negative doppleganger to the electron, but with an opposite electric charge. Dirac came around and proposed the existence of an entire antimatter universe with anti-atoms and anti-stars, even anti-animals. Then in 1932 Carl Anderson detected a particle that fitted the bill, which came to be called the positron. Today physicists believe there are antimatter twins to all the matter particles.

What’s so astounding here is that an abstract equation led to a real-world discovery. The symmetry of the math led physicists to see the possibility of a symmetry in nature. Function followed form.

The lattice of the E-8 symmetry group

The history of physics is replete with other examples. Maxwell’s adherence to principles of symmetry helped him formulate his equations of electromagnetic fields and led to his prediction that light is waves of electric and magnetic fields traveling through space. As I write in my Templeton essay:

This remains one of the most extraordinary and unexpected discoveries in all of physics – in all of science really – born out of nothing more, and nothing less, than a willingness to take conceptual symmetry as a guide to the real world.

Physicists love symmetries because they encode qualities of things that are unchanging. You can think about this by considering a ball. I can turn a ball around in any direction and it still looks the same. As I rotate it in my hands something remains constant – the sphere-ness of the thing endures no matter in what direction I behold it. This isn’t true for an egg, which has a big end and a small end. It’s even less true for a banana, which looks different from every angle.

Mathematicians encode various kinds of sameness and difference with the language of symmetry groups, which was one of my favorite subjects at university. If I were Empress of Education all children would be taught about group theory from an early age by playing with shapes and manipulating objects in their hands.

Modern physicists have come to believe that many phenomena can be described by mathematical symmetries which show how things which appear different are actually various manifestations of some underlying sameness. Particles and antiparticles, for instance, are various manifestations of the same underlying equation. The proposed theory of supersymmetry postulates that all matter-particles (such as the electron and proton) have a force-particle twin (like the photon), and vise versa, that all force-particles (or bosons) have a matter-particle twin (or fermion). So far we haven’t detected any of these “SUSY” siblings, but beauticians like Wilczek believe we’ll see them soon. How could such a beautiful mathematical theory not be true?

Anytime a quality of nature is preserved during a physical transformation, physicists believe there’s a mathematical symmetry to explain what endures. We owe this insight to the German genius Emmy Noether, a contemporary of Einstein, who helped him with the math of general relativity and is probably the greatest physicist most people have never heard of. [She was treated appallingly by a lot of her male contemporaries and by the scientific establishment.]

Symmetry is certainly a virtue if one is looking for what is not changing in the world. In this sense it’s the formalization of Plato and Parmenides’ dream that beyond the veil of mutating appearances there is something eternal in the world, some changeless core which constitutes the “true” reality.

Plato’s yearning for the unchanging has served as a powerful inspiration in modern physics. I wrote about this essentially religious ethos in my book Pythagoras’ Trousers. But it’s worth asking if there are limits to the usefulness of the idea.

Weyl himself, in his delightful 1952 monograph, Symmetry, points to the philosophical problem here. Quoting art historian Dagobert Frey, Weyl notes that symmetry:

“signifies rest and binding, asymmetry motion and loosening, the one order and law, the other arbitrariness and accident, the one formal rigidity and constraint, the other life, play and freedom.”

Beauticians of physics are looking for “rest and binding,” for “order and law,” for “formal rigidity and constraint.” They would literally bind nature. Those who might question this vision - and I include myself here – want to allow nature more “life,” more “play,” more “freedom.”

Whenever some quality of nature is preserved during a physical transformation physicists believe there’s a mathematical symmetry to explain what endures.

Tensions between the beauticians and what I’m going to call the changelings have been present in Western philosophy since pre-Socratic times. Where Parmenides insisted that all change is an illusion, Heraclitus memorably declared that no-one could step into the same river twice, a nice way of saying everything is flux.

The battle between beauticians and changelings is one of the great stories in the history of Western science dating back at least 2,500 years. Plato sided with Parmenides, Aristotle sided with Heraclitus. Aristotelian science, which insisted on the reality of change, held sway over European thinking about the natural world for nearly two millennia. But it began to come undone in the late Renaissance. One way to understand the emergence of modern physics in the 16th and 17th centuries is to see it as the overthrow of the changelings by the beauticians. Platonism and its obsession with “unchanging laws” finally “conquered” Aristotelean ideas about substances in flux. This is the story told in many histories of science.

Another way to look at this is through the lens of aesthetics. Platonists were besotted on certain kinds of mathematical order which they construed to be beautiful – and that’s what they focused on finding. In many ways they succeeded; and are still succeeding today on some fronts. Take for example Wilczek’s prediction of ‘time crystals,’ time-symmetric versions of the usual kind of crystals, which are symmetric structures in space. In 2012 Wilczek proposed there could be quantum structures regularly arranged in time. Lo and behold such weirdness can be constructed, and they may even be useful for quantum computer memory.

Wilczek declares himself proudly as a Platonist. And like other Platonists he’s searching for stasis. But if the core of reality is static then there is no true evolution. Not of anything. Not of life. Not of the universe. Not even thought. This is why many beauticians claim that time is an illusion, and why they say the whole universe is determined from the beginning. Atoms, stars, planets, life, ardvarks, you, me, and every action we’ll ever take are, according to them, pre-encoded in the “laws of nature.” It’s all just a consequence of underlying mathematical laws.

A commitment to symmetry as the ultimate ideal leads, in the end, to a denial of change in any real sense. We changelings stand by change as a genuine and vital phenomenon.

*

I’ll be writing more about these issues in the coming months – and in my new book, which is now in progress. My next post will be a formal anoucnement about the book. In the meantime, if you’re interested in the history of beautician physics, check out my Templton essay.